Lineage-specific growth of SARS-CoV-2 B.1.1.7 during the English national lockdown
Preliminary report.
Harald Vöhringer1, Matthew Sinnott2, Roberto Amato2, Inigo Martincorena2, Dominic Kwiatkowski2, Jeffrey C. Barrett2 and Moritz Gerstung1, on behalf of The COVID-19 Genomics UK (COG-UK) consortium3
1 European Molecular Biology Laboratory, European Bioinformatics Institute EMBL-EBI
2 Wellcome Sanger Institute
3 https://www.cogconsortium.uk
Background: The emerging B.1.1.7 SARS-CoV-2 lineage has proliferated rapidly in the U.K. Here we use a combination of daily local SARS-CoV-2 incidence data and weekly genomic surveillance data from COG-UK to infer its infection dynamics and parameters during English national lockdown from November 5 to December 2 2020.
Methods: A hierarchical Bayesian model is used to jointly model lineage-agnostic spatiotemporal SARS-CoV-2 PCR test data and genomic sequencing data of the B.1.1.7 lineage. This analysis infers the total and lineage-specific temporal incidence in each local authority and estimates the historic basic reproductive ratio R for new and other SARS-CoV-2 lineages per local authority.
Findings: We find strong and consistent evidence that B.1.1.7 proliferated (R>1) during the English lockdown in 87% (213/244) of lower tier local authorities with an average R value of 1.25. At the same time other lineages contracted (R<1) at an average R value of 0.85 in most regions, leading to 83% (203/244) of regions showing B.1.1.7 proliferation while other lineages diminished.
Implications: The emerging B.1.1.7 SARS-CoV-2 lineage spreads faster than its predecessors. It continued to grow during a lockdown in which other lineages shrank. These analyses suggest that stricter measures are required to contain the B.1.1.7 lineage.
Introduction
A new SARS-CoV-2 lineage termed B.1.1.7 (known as VOC202012/01 by Public Health England) was first observed in the U.K. on September 20 in Kent [1]. It has since spread to at least 244/317 English local authorities (based on genome sequencing data until December 13), with a particularly high prevalence in the South East of England, and contributes an ever increasing share of cases locally and nationally. This indicates increased transmissibility relative to other circulating lineages which is estimated to be 1.5-1.7 fold [2-4]. A particular concern is B.1.1.7’s rise during the period of English lockdown between November 5 and December 2 2020, during which SARS-CoV-2 case numbers were generally contracting. It is therefore an urgent question whether the relative B.1.1.7 growth was enabled by biologically increased transmissibility or whether it was facilitated by local failure of lockdown compliance.
Here we test these hypotheses using a hierarchical Bayesian model of lineage-specific spatiotemporal prevalence and R values of B.1.1.7 and other SARS-CoV-2 lineages (Methods). The model is fit to publicly available daily PCR testing data for each of 382 lower tier local authorities (LTLAs) across the U.K. during the period of September 1 to December 22, 2020, as well as aggregated weekly genome surveillance data from 317 English LTLAs (a total of 44,418 viral genomes) from COG-UK covering the period from September 21 to December 13, 2020.
We specifically investigate lineage-specific temporal R values during the period of the English lockdown. The analysis reveals that the B.1.1.7 lineage grew (R>1), while other lineages shrank (R<1) in 200/244 LTLAs. The rate at which other SARS-CoV-2 lineages contracted was similar across areas regardless of the presence of B.1.1.7, providing strong evidence that B.1.1.7 was repeatedly capable of expanding despite lockdown measures sufficient to suppress other SARS-CoV-2 lineages.
Results
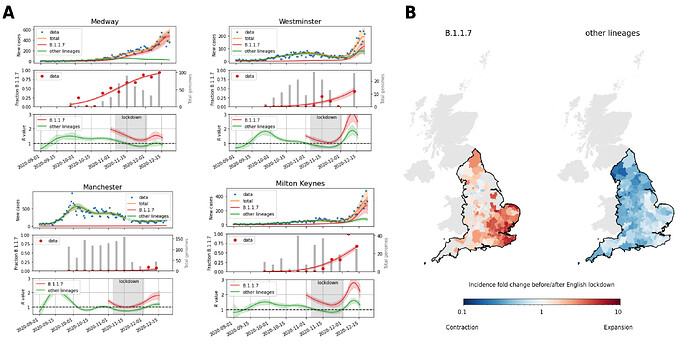
Across regions, the total number of cases (defined here as the number of positive PCR tests) usually showed a rise throughout October, followed by decline during lockdown from November 5 to December 2 and a rise in the weeks before Christmas (four examples shown in Figure 1A). In some LTLAs, however, total cases either remained constant or even increased during lockdown, particularly those in the south east of England. These trends are well recapitulated by the model fits.
Figure 1. Spatio-temporal patterns of SARS-CoV-2 B.1.1.7 growth. A. Example inferences of lineage-specific transmission dynamics based on overall incidence (top; blue dots) and relative B.1.1.7 prevalence (middle; red dots, grey bars show the total numbers of genomes sequenced in each week). Lines depicts fits of lineage specific incidence (top) and relative prevalence (middle). The bottom row shows the associated lineage-specific R values with the English lockdown from November 5 to December 2 highlighted in grey. Shaded areas are 95% highest density posterior intervals. B. Inferred strain-specific incidence fold changes of B.1.1.7 and other SARS-CoV-2 lineages between start and end of the English lockdown (5.11. to 2.12.2020). Light grey areas have no B.1.1.7 lineage information available. England is highlighted by a black outline.
The relative prevalence of B.1.1.7, as a fraction of all genomes sequenced, was initially low in all local authorities and continued to rise as evidenced by genomic surveillance data from COG-UK. Based on the relative prevalence of B.1.1.7 in each LTLA and the case total, the absolute number of B.1.1.7 cases was estimated, revealing that the lack of total case reduction in some areas can be explained by a high prevalence and persistent growth of B.1.1.7 rather than general failure of viral containment (Figure 1A). This pattern is also evident in the maps showing the inferred fold change of B.1.1.7 and other SARS-CoV-2 lineage across the lockdown period, which indicate that B.1.1.7 actively expanded, while other lineages contracted in most LTLAs (Figure 1B).
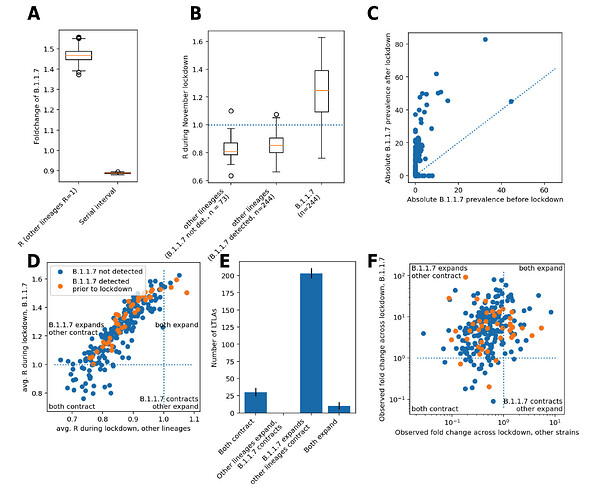
The estimated R value of B.1.1.7 was approximately 1.47-fold higher (95% CI 1.41-1.53) than that of the collection of other circulating lineages, broadly consistent with previous reports (Figure 2A). Across time the R value of B.1.1.7 increased largely proportionally to that of the other lineages by the aforementioned factor of approximately 1.5. This scaling was remarkably consistent across different LTLAs (Figure 1A; IQR 1.43-1.54). Further, a moderate level of non-linear scaling between the R values was observed (exponent 1.127; CI 1.12-1.134), which may be interpreted as a shortening of the serial interval from an average of 6.5d assumed for other SARS-CoV-2 lineages to 5.8d for B.1.1.7 (Methods).
Figure 2. Biological parameters and B.1.1.7 lineage-specific growth during the English lockdown. A. Biological parameters of B.1.1.7 relative to other SARS-CoV-2 lineages. B. Lineage-specific average R values during English lockdown from November 5 to December 2, 2020. C. Fold change of absolute B.1.1.7 prevalence before and after lockdown, defined as observed relative B.1.1.7 prevalence times total number of positive PCR tests scaled to population size/100k. The dotted line denotes the diagonal, values above it signify an increase. D. Scatterplots of estimated lineage-specific R values for LTLAs with detected B.1.1.7 prior to lockdown. E. Viral growth patterns from lockdown across 246 LTLAs. F. Scatterplot of lineage-specific fold change during lockdown, defined as the odds ratios of raw case number and B.1.1.7 prevalence before and after lockdown.
During the period of English lockdown from November 5 to December 2 the temporal average R value of other lineages, considered collectively, was below the critical value of 1 in 96% of LTLAs (median R = 0.85, IQR 0.79-0.91), and R was at least temporarily below 1 in 99% of LTLAs. Of note this was independent of the presence of B.1.1.7 at the onset of lockdown (Figure 2B). This suggests that the English lockdown was broadly effective against the previously predominant SARS-CoV-2 lineages.
In contrast, the estimated R value of B.1.1.7 during English lockdown was on average above 1 in 88% of LTLAs (median R = 1.25, IQR 1.09-1.39) and never below 1 in 64% of cases. This implies that B.1.1.7 case numbers grew in absolute terms rather than gaining a relative advantage from slower contraction. The fact that B.1.1.7 actively expanded is also supported by the fact that raw B.1.1.7 case numbers, scaled by their proportions based on genomic surveillance, increased over the lockdown period (Figure 2C).
In 83% (203/244; CI 81-86%) of LTLAs a rise (R>1) of B.1.1.7 and simultaneous decline of other lineages (R<1) was noted. This demonstrates that failure to contain B.1.1.7 was generally not caused by overall failure of SARS-CoV-2 control but rather by its inherent biological properties causing a higher transmissibility of the virus (Figure 2D,E). This pattern of B.1.1.7 strain-specific growth during lockdown is supported by a model-agnostic analysis of the change in raw case numbers, calculated simply by multiplying the number of positive PCR tests in a given LTLA by the proportion of B.1.1.7 genomes in the weeks prior to and after the lockdown (Figure 2F).
The model also suggests that B.1.1.7 R values tended to be slightly lower in areas with lower baseline R, suggesting that more efficient suppression of the new lineage could be achieved by stricter rules and/or compliance. A certain degree of correlation between the two R values, however, is inherent in the model parameterization, which assumes a varying degree of proportionality between the two R values in each LTLA. Weak support of this claim provides the correlation of the fold changes of B.1.1.7 and other lineages pre and post lockdown (Spearman’s rho = 0.32; P = 4 x 10–7; Figure 2F).
Conclusion
The rise of relative B.1.1.7 prevalence across regions since its first discovery indicates a strong transmissibility advantage over previous circulating lineages. A particular question is whether B.1.1.7. spread during English lockdown due to a general failure of viral containment in particular areas or because of a lineage specific selective advantage.
The analysis presented here demonstrates a consistently higher R value for B.1.1.7 by a factor of 1.47 at any given time. In relation to the English lockdown the data show that other lineages contracted during lockdown with an R value of 0.85, largely independent of B.1.1.7 presence. Conversely, B.1.1.7 grew in absolute terms during lockdown, at an average R of 1.25. Thus, the spread of B.1.1.7 was due to a lineage-specific transmissibility advantage, rather than general inefficacy of viral control. There is some weak evidence that the rate of B.1.1.7 growth was lower in areas with greater lockdown efficiency.
The implications of these findings are that containment of B.1.1.7. is likely to require stricter lockdown policies and compliance than applied during the English lockdown in November 2020. As B.1.1.7 is likely to have proliferated to other countries, similar measures may be required in other countries.
Limitations
The inference is based on dense PCR testing but relatively sparse genomic surveillance data covering a shorter period. For that reason a parametric form linking the R values of the novel and other lineages was used. The conclusion that B.1.1.7 grew in many regions during lockdown is supported, however, in a model agnostic way by the absolute case count prior to and after lockdown, scaled by local incidence (Figure 2C). In a similar fashion one finds a concomitant decrease of other strains over the lockdown period by applying the same rationale to the observed proportion of other lineages (Figure 2F).
The modelled curves are smoothed over intervals of approximately 10 days using 8 cubic splines, creating a possibility that later time points influence the period of investigation and causing a certain waviness of the R value pattern. An alternative parameterization using piecewise linear basis functions per week (i.e., constant R values per week) leaves the overall conclusions and extracted parameters broadly unchanged.
While the proportional relationship between lineage-specific R values is well supported by the data across LTLAs, further data is needed to assess whether stricter lockdown or better compliance with existing tier 4 rules is sufficient to suppress B.1.1.7. to R values below 1.
The definition of R values used here is based on a fixed serial interval $\bar\tau$ between consecutive infections. Accounting for a distribution of $\bar\tau$ produces qualitatively similar results.
As the total incidence is modelled based on positive PCR tests it may be influenced by the number of tests conducted, which approximately double between September and December 2020. This can potentially lead to a time trend in baseline R. During the period of lockdown, however, the number of daily PCR tests was approximately constant at around 320,000.
Methods
Daily SARS-CoV-2 PCR test result data (newCasesBySpecimenDate) was downloaded from gov.uk spanning the date range from 2020-09-01 to 2020-12-22 for 382 lower tier local authorities (downloaded on 2020-12-27, excluding the last 4d due to incompleteness).
Lineage prevalence was computed from 44,445 genome sequences collected as part of random surveillance of positive tests of residents of England from four pillar 2 Lighthouse Labs. The samples were collected between 2020-09-21 and 2020-12-13. Lineage assignments were made using the COG-UK grapevine [5]. We aggregated the number of B.1.1.7 sequences and sequences from all other lineages by week and local authority. 246 out of 382 LTLAs had genomic information indicating presence of B.1.1.7 during the surveillance period.
A hierarchical Bayesian model was used to fit the local incidence data of SARS-CoV-2 in a given day in each local authority and jointly estimate the relative historic prevalence and transmission parameters of the new B.1.1.7 lineage.
In the following all bold variables are vector-valued across LTLAs; $t$ denotes time and is measured in days. The subscript 0 refers to all other lineages, while 1 denotes B.1.1.7. The logarithmic temporal incidence $\boldsymbol{\mu}_0(t) = \mathrm{log} \boldsymbol{I}_0(t)$ of all other SARS-CoV-2 lineages was modelled using 8 cubic spline basis functions in each of 382 LTLAs,
$\boldsymbol{\mu}0 (t) = \sum{j} \boldsymbol{\beta}_{j} {f}_j(t),$
where ${f}_j(t)$ is the $j$ -th basis function. The symbol $\boldsymbol{N}$ is the population size in a given LTLA and $\boldsymbol{\beta}_j$ are the regression coefficients for the $j$th spline function in each local authority. The associated time dependent R value is
$\log{\boldsymbol{R}_0(t)}=\frac{d \log{\boldsymbol{I}_0}}{d\tau}=\frac{d \log{\boldsymbol{I}_0}}{d t}\frac{d t}{d\tau}=\bar\tau\sum_j \boldsymbol{\beta}_j{f}'_j({t})$
where $\tau$ is time measured in units of the serial interval (approx $\bar\tau$ = 6.5 days) [6] and ${f}'_j({t})$ the first derivative of the $j$th cubic spline basis function.
For the 317 English LTLAs with genomic information, the R value of the B.1.1.7 lineage was modelled as
$\log{\boldsymbol{R}_1(t)}=\boldsymbol{a}\log{\boldsymbol{R}_0(t)}+\boldsymbol{b},$
implying that $\boldsymbol{R}_1(t) = {\boldsymbol{R}_0(t)^\boldsymbol{a}} \times e^\boldsymbol{b}$. The typical fold change in R value can thus be derived from $e^\boldsymbol{b}$, consistent with a constant selective advantage. The parameter $\boldsymbol{a}$ can be interpreted as the inverse fold change of the average serial interval $\tau$ and induces a non-linear scaling of $\boldsymbol{R}_1(t)$. It follows that the logarithmic incidence $\boldsymbol{\mu}_1(t) = \int \boldsymbol{R}_1(t) dt$ can be expressed as
$\boldsymbol{\mu}_1(t) = \boldsymbol{a} \boldsymbol{\mu}_0(t) + \boldsymbol{b} {t} + \boldsymbol{c}$
The parameter $\boldsymbol{c}$ measures an offset of B.1.1.7 in the logarithmic incidence. The parameters $\boldsymbol{a}$ are modelled across LTLAs by a log Normal prior distribution with shared mean $\bar a$, while the parameters $\boldsymbol{b}$ are modelled with a Normal prior distribution with shared mean $\bar b$.
The total expected incidence was $\boldsymbol{I}(t)=\boldsymbol{I}_0(t)+\boldsymbol{I}_1(t)$. Here $\boldsymbol{\mu}_1(t)$ was set to 0 for LTLAs without genomic data and only the total incidence rather than strain-specific incidence modeled. $\boldsymbol{I}(t)$ was fitted to the observed number of positive daily tests $\boldsymbol{X}(t)$ by a negative binomial distribution with dispersion $\boldsymbol{\rho}$.
$\boldsymbol{X}(t)\sim\text{NB}(\boldsymbol{I}(t), \boldsymbol{\rho}).$
The expected relative prevalence of the new lineage is $\boldsymbol{p}_1(t) = {\boldsymbol{I}_1(t)}/\boldsymbol{I}(t)$. Note that for $\boldsymbol{a}=1$, $\boldsymbol{p}_1(t)$ equals a logistic equation with parameter $\boldsymbol{b}$. The proportion of B.1.1.7 genomes was fitted to the number of weekly B.1.1.7 genomes $\boldsymbol{Y}(t)$ in each LTLA by a binomial distribution.
$\boldsymbol{Y}(t)\sim\text{Bin}(\boldsymbol{p}_1(t), \boldsymbol{G}(t)).$
Where $\boldsymbol{G}(t)$ are the total number of genomes sequenced from the given LTLA in each week. The model further exploits the spatial structure of the data by using hierarchical prior distributions for $\boldsymbol{\beta}$ on UTLA level (if available) and country level.
The model was implemented in numpyro and fitted using stochastic variational inference. code is available at https://github.com/gerstung-lab/sarscov2-b117.
Acknowledgements
COG-UK is supported by funding from the Medical Research Council (MRC) part of UK Research & Innovation (UKRI), the National Institute of Health Research (NIHR) and Genome Research Limited, operating as the Wellcome Sanger Institute. We would like to thank our colleagues at EMBL-EBI, the Wellcome Sanger Institute and from COG-UK for stimulating discussions and helpful comments on this report.
Data availability
PCR test data are publicly available at https://coronavirus.data.gov.uk/. SARS-CoV-2 genome data can be obtained from https://www.cogconsortium.uk/data/.
References
- Preliminary genomic characterisation of an emergent SARS-CoV-2 lineage in the UK defined by a novel set of spike mutations, URL: https://pando.tools/t/preliminary-genomic-characterisation-of-an-emergent-sars-cov-2-lineage-in-the-uk-defined-by-a-novel-set-of-spike-mutations/563
- Public Health England, Investigation of novel SARS-COV-2 variant Variant of Concern 202012/01
https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/947048/Technical_Briefing_VOC_SH_NJL2_SH2.pdf - Minutes of NERVTAG meeting on SARS-CoV-2 variant under investigation VUI-202012/01. URL https://app.box.com/s/3lkcbxepqixkg4mv640dpvvg978ixjtf/file/756963730457
- Nicholas Davies et al. Estimated transmissibility and severity of novel SARS-CoV-2 Variant of Concern 202012/01 in England. URL https://cmmid.github.io/topics/covid19/uk-novel-variant.html
- https://github.com/COG-UK/grapevine/tree/master/docs
- Bi Q et al. (2020) Epidemiology and transmission of COVID-19 in 391 cases and 1286 of their close contacts in Shenzhen, China: a retrospective cohort study. Lancet Infect Dis 20, 911–919.